Temporal Extension: Entropic Mechanics Across Time

Just as $\eta$ quantifies the additional thermodynamic cost from position, chaos dynamics offer a framework to describe how that cost evolves through time. The same microsecond changes that feel random from the inside are revealed, in retrospect, as mathematically deterministic. Like the rock in a pond, the outcome is not random—but is wholly dependent on when, where, and what it strikes. This temporal dimension transforms static positional energy multiplier calculations into dynamic predictions.

Conscious Chaos: A theoretical synthesis exploring how conscious agents navigate entropic constraints and systemic boundaries through time. Integrates observer-dependent energy multiplier $\eta$, intention vectors $\vec{V}$, percolation theory, and time-sensitive perturbations to model how time enables navigation rather than mere obedience to universal constraints.

For how time and information serve as navigation tools beyond normal entropic bounds, see Time and Information: The Navigation Tools.

---

The Pond and the School of Fish

Traditional change models often limit their analysis to surface-level phenomena. Most change models focus on the surface: a rock hits the water, ripples form. But Conscious Chaos examines deeper dynamics: what happens when that rock disrupts a school of fish just below the surface?

The mathematical framework indicates two distinct response layers:

• Surface physics: Wave propagation follows predictable patterns
• Subsurface dynamics: Position-dependent thermodynamic responses

Predators near the surface experience the ripple as opportunity $\eta = 0.2$, while bottom-feeders scatter in panic $\eta = 0.8$—the same perturbation creating opposite responses based purely on position.

This layered response indicates that identical perturbations cause divergent energy expenditure depending on position. Modeling collective outcomes therefore requires integrating both positional energy multiplier and time dimensions to capture the full dynamics.

---

Wolf Pack in Yellowstone

Natural systems provide compelling examples of how chaos dynamics interact with positional energy multiplier. Consider the thermodynamic reality of wolf pack hunting dynamics. When prey moves unpredictably, each wolf’s response depends critically on their hierarchical position. Alpha wolves at $\eta = 0.2$ can efficiently coordinate the pack’s response, while omega wolves at $\eta = 0.8$ must expend significantly more energy to maintain their position in the pursuit—a difference that compounds over time.

This natural system demonstrates how chaos dynamics interact with positional energy multiplier. A prey animal’s sudden direction change (the perturbation) creates exponentially different energy costs based on pack position—exactly what the temporal $SEC$ equation predicts. The wolf pack example illustrates how nature itself operates according to the principles of conscious chaos, with position determining the thermodynamic cost of responding to unpredictable perturbations.

For detailed thermodynamic analysis of wolf pack hierarchies, see Wolf Pack Thermodynamics.

---

Temporal Navigation Within Bounded Systems

Time provides the dimension through which consciousness navigates entropic constraints. Unlike matter and energy which must obey boundaries directly, time enables:

• Future projection: Testing possibilities without thermodynamic commitment
• Memory formation: Learning from past navigation attempts
• Pattern recognition: Identifying cycles within bounded systems
• Coordination planning: Synchronizing multiple agents’ navigation

This temporal freedom explains why evolution selected consciousness as the universe’s navigation mechanism—it can explore possibility spaces that purely physical systems cannot access.

---

Integration of Temporal Dynamics

Mathematical formalization provides a framework for understanding how navigation unfolds through time. The time derivative of System Entropy Change captures how transformations accelerate or decay under time-sensitive conditions.

$$\frac{dSEC}{dt} = \hat{O} \times \vec{V} \times f(\eta) \times [1 + \alpha \cdot \sin(\omega t)]$$

Components:

• $\hat{O} \text { (Operations cost)}$: thermodynamic energy multiplier reflecting the energy hierarchy required to perform each operation ($\hat{O}_M^{(1)}$, $\hat{O}_J^{(2)}$, $\hat{O}_S^{(3)}$). Values represent physical grounding in energy requirements
• $\vec{V} \text { (Vector of shared conscious intent)}$: mathematical vector with magnitude (strength of collective alignment, $0$ to $1$) and direction (positive for entropy reduction, negative for increase). Exhibits wave properties where vectors can sum or interfere constructively/destructively. Represents collapsed state after social computation filters competing interpretations into shared reality
• $f(\eta)$: Positional energy multiplier’s dampening effect where $f(\eta) = 1/(1+\eta)$. $\eta$ represents thermodynamic cost required to perform operations from position. Like mass in $F=ma$, $\eta$ must be known to predict outcomes.
• $\alpha \text { (Amplitude of chaotic perturbations)}$: Environmental stress, volatility.
• $\omega \text { (Frequency of oscillations)}$: Rate of system changes.

This theoretical formulation integrates three mathematical domains:

• Observer-dependent mathematics: From Information Physics
• Chaos sensitivity: From nonlinear dynamics (Lorenz systems, logistic maps)
• Critical transitions: From percolation and phase transition theory

The equation indicates that conscious systems don’t just have static entropy values—they evolve through time with sensitivity to both position and perturbations. This temporal dimension transforms static understanding into dynamic prediction capability.

Visual Framework

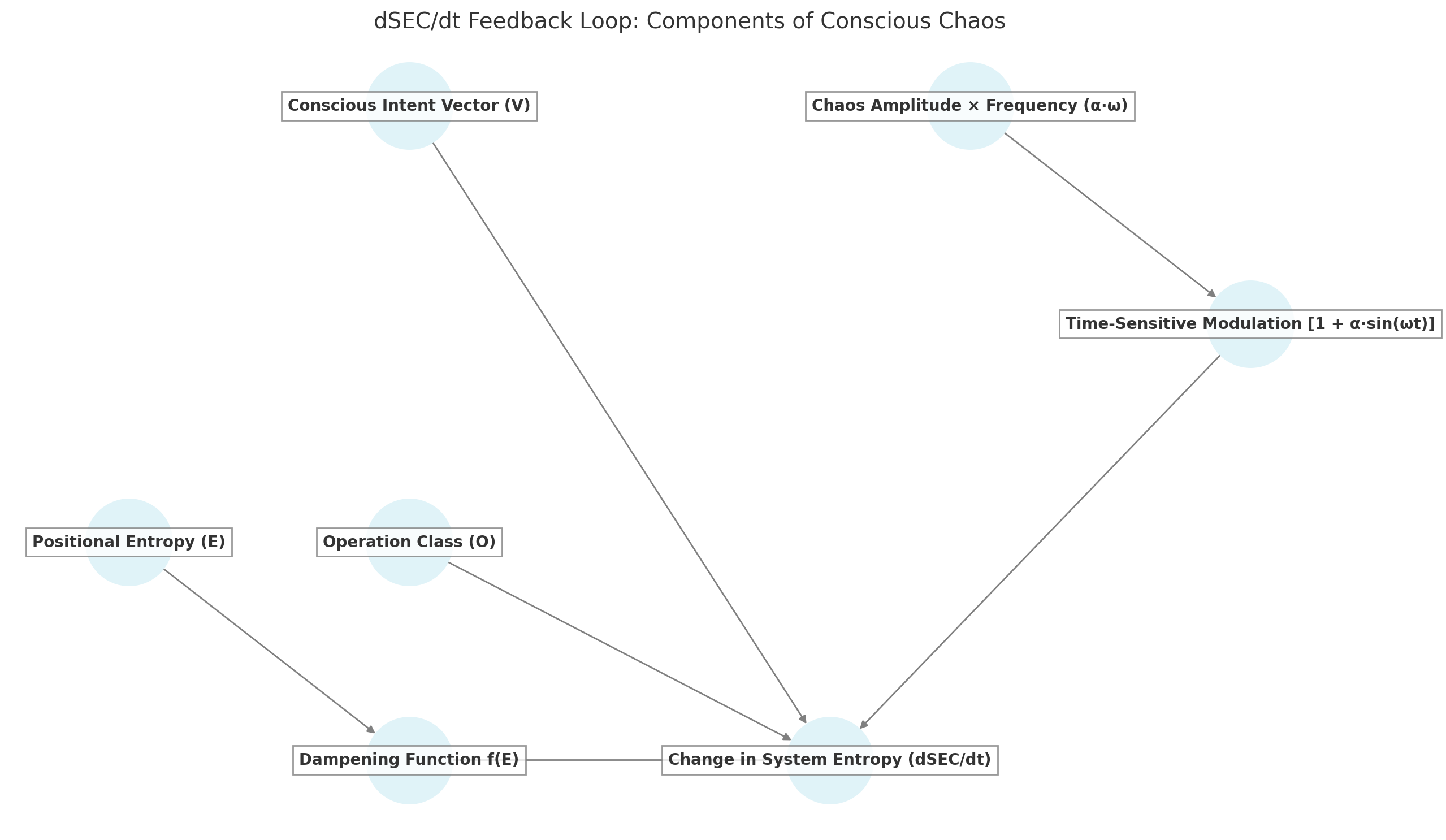Components of Conscious Chaos: How positional energy multiplier, operations, conscious intent, and chaotic perturbations combine to drive temporal system entropy changes

The feedback dynamics reveal how each component influences the rate of entropy change. Position constrains available energy, operations determine the type of change, conscious intent provides direction, and temporal perturbations add the chaos element that makes outcomes sensitive to timing.

Mathematical Parallels

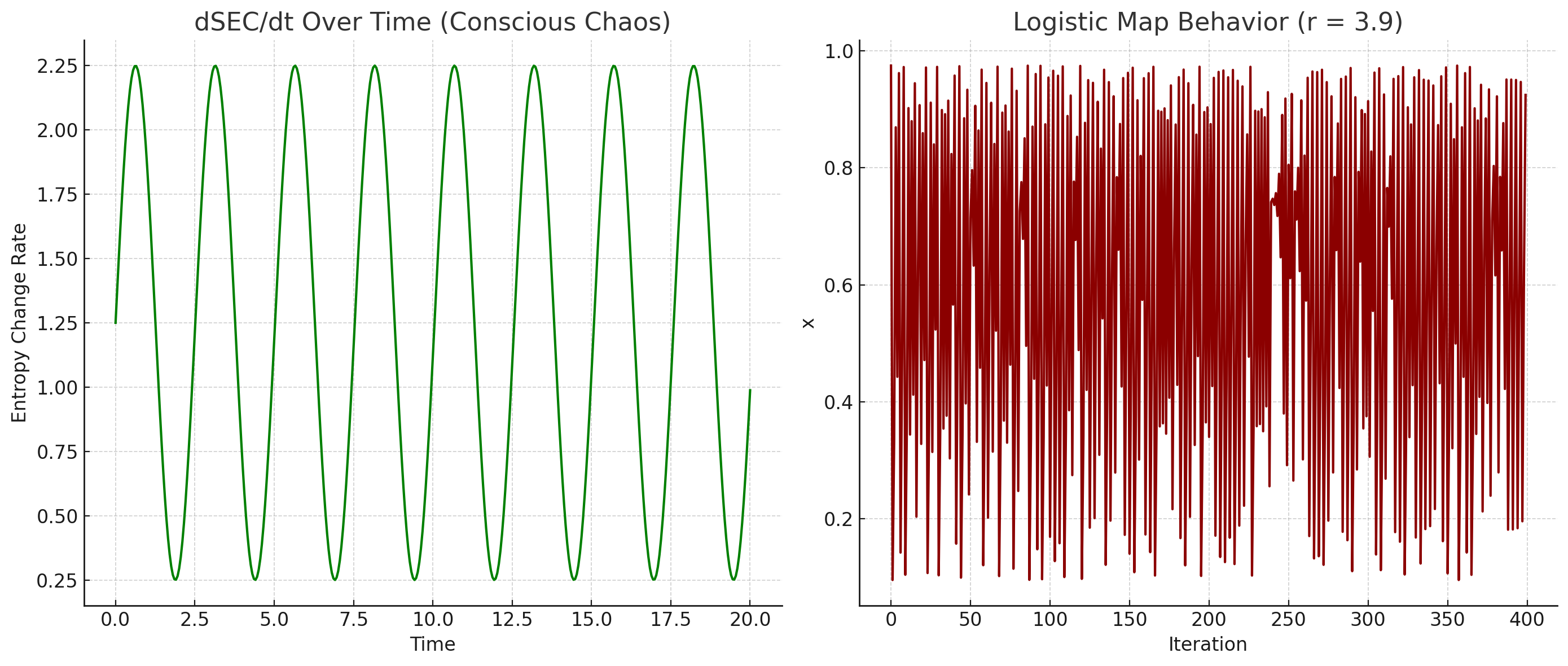Temporal $SEC$ dynamics compared to classic chaos: Regular oscillations in low-perturbation systems (left) versus chaotic behavior similar to the logistic map at $r=3.9$ (right)

This comparison illustrates how conscious systems transition from predictable oscillations to chaotic behavior as perturbation parameters increase. The mathematical similarity to established chaos models indicates that consciousness navigating entropy follows universal nonlinear dynamics.

---

Applications

Real-world systems exhibit behaviors that align with the temporal $SEC$ framework. The temporal $SEC$ equation indicates several theoretical applications across different domains.

The framework applies to diverse systems where entropy and time interact:

• Innovation environments: Silicon Valley versus Renaissance Florence respond differently to identical economic shocks based on their current $\eta$ values, $\vec{V}$ alignment, and oscillatory states. A market crash catalyzes innovation in low-entropy Florence while paralyzing high-entropy Silicon Valley.
• Crowd dynamics: Phase transitions in collective behavior reflect rapid $dSEC/dt$ spikes when $\vec{V}$ vectors align and systems cross percolation thresholds. Mathematical models indicate riots are not random but follow predictable chaos patterns.
• Organizational collapse: System failure emerges exponentially rather than linearly when multiple factors amplify: high $\eta$ (positional energy multiplier), negative $\vec{V}$ (destructive intent), high $\alpha$ (environmental volatility), and increasing $\omega$ (accelerating change cycles).

These applications indicate that temporal entropy dynamics govern phenomena across scales, from individual organizations to entire civilizations.

---

Validation Requirements

Disclaimer: This theoretical framework requires extensive empirical validation before acceptance as established scientific theory. The synthesis and mathematical relationships outlined above need systematic testing through:

• Controlled experiments measuring temporal SEC dynamics across different system types
• Statistical validation of chaos theory alignments in conscious system behavior
• Laboratory verification of position-dependent temporal perception effects
• Cross-domain studies confirming perturbation sensitivity patterns
• Mathematical verification of the temporal SEC equation parameters
• Neurological studies validating consciousness as temporal navigation mechanism
• Field studies tracking entropy evolution in real organizational systems
• Peer review and independent theoretical verification

While Conscious Chaos offers compelling explanatory power and mathematical consistency, it represents a speculative theoretical synthesis that must undergo rigorous scientific validation through empirical evidence, experimental confirmation, and theoretical scrutiny before acceptance as established science.

---

Conclusion

The apparent contradiction between consciousness and chaos dissolves when recognizing time as a navigation tool for bounded systems. While matter and energy remain fully constrained, time’s unidirectional flow enables planning and projection—allowing consciousness to explore possibility spaces before committing physical resources. What appears random reflects unmeasured sensitivity to initial conditions within these navigational calculations.

In this theoretical framework, the observer’s position determines temporal perception itself. Whether an event feels sudden, inevitable, or invisible depends not on clock time but on the entropic viewpoint—high-$\eta$ positions experiencing time differently than low-$\eta$ positions due to thermodynamic constraints on information processing.

This synthesis attempts to bridge theoretical and established domains:

• Consciousness: Contributes intentional navigation through entropic landscapes
• Entropic mechanics: Provide the positional constraints that shape possibilities
• Chaos mathematics: Add the temporal sensitivity that creates unpredictability

The result indicates a unified framework where conscious beings navigate inherently chaotic systems, with outcomes determined by the intersection of position, intent, and timing. Like the rock in the pond, effects ripple differently based on where, when, and how the perturbation occurs.

The mathematical convergence between Information Physics and chaos theory creates a unified framework for understanding conscious systems navigating temporal dynamics.